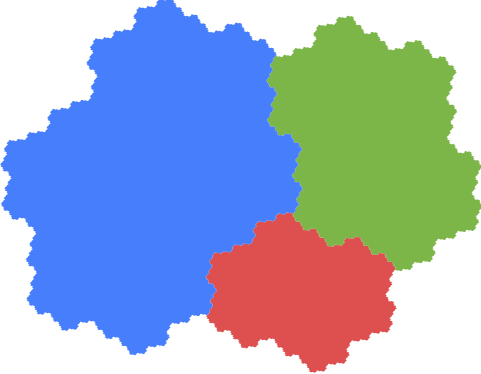
La fractale de Rauzy

La fractale de Rauzy est un domaine du plan qui, comme son nom l’indique, possède une structure fractale. Conçue par le mathématicien français Gérard Rauzy (1938 -2010), cette fractale est le fruit de ses recherches en théorie des nombres et en systèmes dynamiques, domaines où il a étudié les itérations de transformations mathématiques, en lien avec l’informatique. Gérard Rauzy a également fondé à Marseille un groupe de recherche du CNRS spécialisé dans les mathématiques discrètes. Il est à l’origine du Centre International de Rencontres Mathématiques (CIRM), un centre réputé pour l’accueil de colloques, de conférences et d’activités mathématiques variées. Le CIRM est un lieu de rencontre pour des mathématiciens du monde entier, favorisant les recherches collaboratives en binômes. On pourrait le comparer à une « Villa Médicis des mathématiques » en raison de son dynamisme et de son programme riche : chaque semaine, il accueille divers événements et reçoit environ 4 700 visiteurs par an.

La fractale de Rauzy provient de l’étude de problèmes de théorie ergodique en lien avec la théorie des nombres et l’informatique. Le problème initial consiste à déterminer comment approcher au mieux une droite irrationnelle. Ce problème découle de la nécessité de représenter une droite sur un écran d’ordinateur, avec la contrainte de n’utiliser qu’un ensemble discret de points, c’est-à-dire les pixels. Ces pixels sont répartis de façon régulières dans l’espace de sorte qu l’on peut supposer qu’ils sont répartis tels les points à coordonnées entières $\mathbb Z^d$ dans l’espace. Pour une droite passant par deux de ces points, le principe est assez simple: il s’agit de sélectionner les points du réseau $\mathbb{Z}^d$ les plus proches de la droite entre ces deux points. Il n’y a qu’un nombre fini de choix à faire, ce qui permet de procéder raisonnablement. On répète ensuite ces choix par translations pour approximer la droite à l’infini. Cependant, la situation se complique lorsque l’on souhaite représenter une droite qui ne passe au plus une fois sur un de ces points du réseau. ne droite qui ne passe par aucun des points du réseau ou qui le fait au plus une fois. On parle alors de droite irrationnelle, contrairement au cas précédent où les coefficients de l’équation de la droite sont des entiers. En dimension deux, la pente de cette droite est un nombre irrationnel. On pourrait partir du même principe et de choisir des points du réseau qui approximative au mieux une droite irrationnelle, mais il y a une infinité de choix à faire et il faut décrire plus précisément par ce que l’on entend par “approximer au mieux la droite”. En fait il n’existe pas de solution optimale en toute généralité. Cependant, dans certains cas particuliers, on peut utiliser judicieusement certaines propriétés.

Par exemple dans le cas où la droite irrationnelle est un espace propre instable d’une matrice de type Pisot, il existe un algorithme relativement simple et efficace pour bien approcher la droite par une ligne brisée composée de points à coordonnées entières. Rappelons ce qu’on entend par matrice de type Pisot¹: il s’agit d’une matrice matrice à coefficients entiers positifs qui possède une unique valeur propre $\beta$ dont le module est strictement supérieur à 1, tandis que les autres valeurs propres ont des modules strictement inférieurs à 1. De plus, toutes les autres valeurs propres sont des conjugués algébriques de $\beta$ , c’est-à-dire qu’elles sont également des racines du même polynôme caractéristique que $\beta$ . Cela impose des conditions arithmétiques spécifiques sur le nombre $\beta$ qui est un nombre algébrique appelé nombre Pisot en référence à Charles Pisot (1910-1984) qui les a étudié. On notera en particulier que $\sqrt{2}$ n’est pas un nombre Pisot car son conjugué n’est pas de module plus petit que un.

Par exemple en prenant la matrice

$M= \begin{pmatrix}1 & 1 &1 \\1 & 0 &0 \\0 & 1 & 0\end{pmatrix}.$

Sa valeur propre de module maximale est $\beta= 1,8392 \ldots$ qui vérifie l’équation $\beta^3 + \beta^2 +\beta -1 =0$ (c’est le polynôme charactéristique de la matrice $M$ ). Son espace propre est engendré par le vecteur

$v_\beta= \begin{pmatrix} \beta^2 \\ \beta \\ 1\end{pmatrix}.$

G. Rauzy a alors proposé l’algorithme suivant de sélection des points. On commence par engendrer une suite infinie de $1,2$ , et $3$ , dite de Tribonacci. de la façon suivante:
à $1$ on substitue le mot $12$ ,
à $2$ on substitue le mot $13$ ,
à $3$ on substitue le mot $1$ .

On part de la lettre $1$ et on itère la substitution décrite au-dessus. On obtient alors
$1$
$12$
$1213$
$1213121$
$1213121121312$
$\vdots$
La suite limite infinie $(t_n)_{n\ge 0}$ que l’on obtient à la limite est la suite de Tribonacci. Les nombres de $1$ , de $2$ et de $3$ dans lors des différentes étapes forme une suite récurrente liénaire d’ordre 3. C’est une généralisation de la fameuse suite de Fibonacci, le terme « Tribonacci » fait alors référence à cet ordre 3.

À partir de cette suite, on considère la ligne brisée dans l’espace $\mathbb R^3$ donnée par la succession de vecteurs $(\sum_{i= 0} ^n e_{t_i})_{n\ge 0}$ où les vecteurs $e_1$ , $e_2$ , et $e_3$ désignent la base canonique de $\mathbb R^3$ . Du fait des propriétés d’hyperbolicité de la matrice (il n’y a qu’une valeur propre agissant par dilatation, les autres agissant par contraction) cette ligne brisée est à distance bornée de la direction propre associé à la valeur propre $\beta$ de module maximal. Pour comprendre un peu plus ce qu’il se passe, on projette, parallèlement à la direction dilatante, cette ligne sur les espace propre supplémentaires. La fermeture de cet ensemble de points donne la fractale de Rauzy.

illustration de la construction de la fractale de Rauzy.
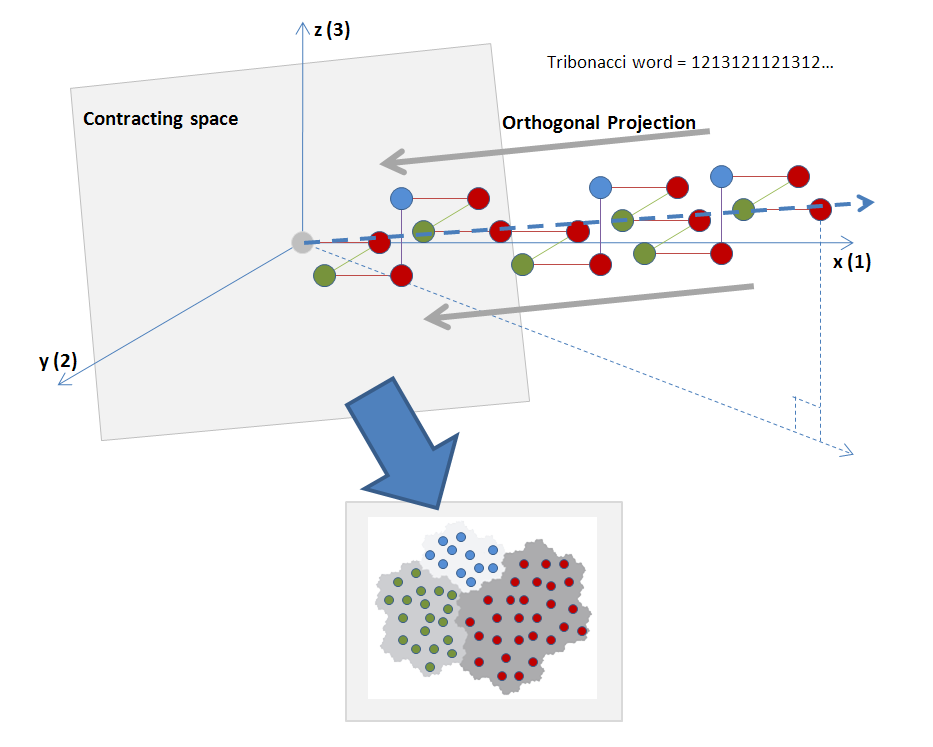
source : wikipedia

Cette fractale possède quelques propriétés remarquables :

Elle est stable par échange de morceaux : la fractale peut être décomposée en trois sous-ensembles, chacun étant également une fractale homothétique à l’ensemble global. Ces sous-ensembles peuvent être translatés pour obtenir différentes décompositions de la fractale.
Elle a des propriétés d’auto-similarité : elle peut être recouverte par trois copies d’elle même (des homothéties) réduites de facteur 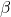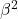$\beta$ , $\beta^2$ et $\beta^3$ .
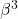Pavage du plan : la fractale pave le plan par des copies obtenues par translation, et ce de manière périodique, c’est-à-dire selon un réseau de translations. Cette capacité est particulièrement surprenante, car un polygone convexe ayant plus de sept côtés ne peut pas paver le plan. Alors une fractale, c’est sans espoir a priori !

Grâce à cette procédure très algorithmique, il est possible de faire des programmes pour approcher assez bien la fractale. Par exemple sur le site kits mathématiques on trouvera les plans pour pouvoir effectuer une découper laser (d’un contreplaqué ou d’une plaque PVC) pour obtenir des fractales des Rauzy. On peut alors tester les propriétés mentionnées (avec des élèves par exemple). De plus cela permet d’avoir une intuition de ce qu’est une fractale avec ses bords irréguliers. On peut imaginer également faire un puzzle (un pavage) avec ces pièces. C’est une expérience assez surprenante et contre-intuitive. On peut également observer à partir des pavés en bois qu’un fractal est l’union de trois homothéties de la même fractale.

Il existe également beaucoup de variantes de cette construction.

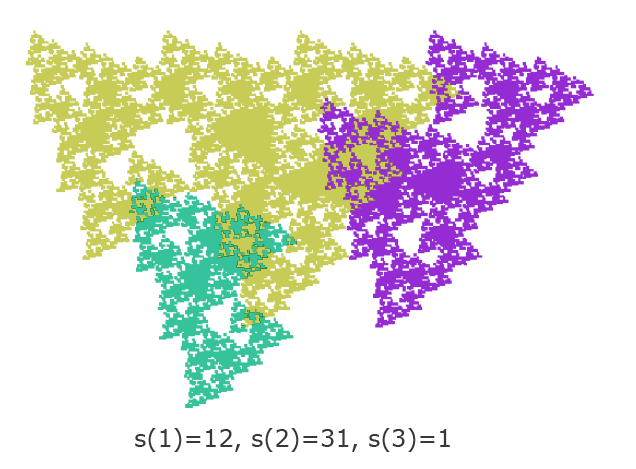
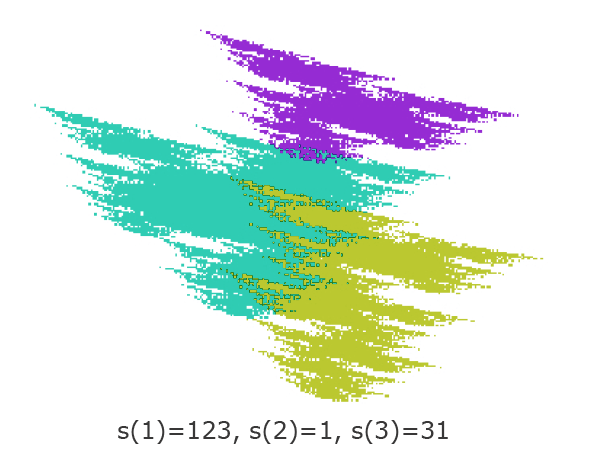
Le lecteur intéressé trouvera plus d’informations dans les références mentionnées plus bas.

Références

N. P. Fogg – Substitutions in dynamics, arithmetics and combinatorics, Lecture Notes in Math., vol. 1794, Springer, 2002.
Page Web de Timo Jolivet
G. Rauzy Nombres algébriques et substitutions, Bulletin de la Société Mathématique de France, 110: 147-178, 1982
Propriétés géométriques des fractales de Rauzy par A. Siegel et P.Arnoux

Le très riche théorème de Perron-Frobenius stipule qu’une matrice à coefficients strictement positifs admet une unique valeur propre de module maximale, il admet un vecteur propre à coefficients strictement positifs, et son l’espace propre associé est de dimension 1 ↩︎

Brochure de l'IREM de Picardie

Institut de Recherche sur l'Enseignement des Mathématiques de Picardie

Références

Laisser un commentaire Annuler la réponse