Philippe Le Moult
Professeur de Mathématiques
lycée Pierre d’Ailly de Compiègne
Philippe-Gerard.Le-Moult@ac-amiens.fr
Mathematics may be defined as the subject in which we never know what we are talking about,
Bertrand Russell (1872 – 1970)
nor whether what we are saying is true.
« Abstraire et formaliser », voici deux verbes bien connus des étudiants en mathématiques sans qu’ils n’en perçoivent toujours le sens profond. Le propos de cet exposé est de fournir des clés pour comprendre les mécanismes de l’abstraction mathématique en dégageant son cheminement naturel. La formalisation ne constitue que l’étape finale de ce processus. Nous verrons également que ce processus s’inscrit dans une histoire longue de plusieurs siècles. Cet exposé s’adresse à tous ceux que les mathématiques intéressent.
Il pourra être utile aux enseignants du secondaire et aux étudiants de premier cycle qui y trouveront des explications pour comprendre les changements de paradigmes qui jalonnent l’histoire et l’enseignement actuel des mathématiques. Cet exposé se termine par une introduction à la théorie des modèles (un niveau L1 en mathématiques sera sans doute nécessaire à sa pleine compréhension). Des rudiments de cette théorie permettent de mieux comprendre le rôle de la théorie des ensembles dans les mathématiques modernes.
I. QUALITES ET OBJETS ABSTRAITS : LES CRÉATIONS DE L’ABSTRACTION USUELLE
Le verbe « abstraire » signifie séparer, isoler. L’abstraction est un acte créatif. L’abstraction usuelle crée des propriétés. Certaines de ces propriétés sont appelés définitions car elles créent des objets abstraits.
La création de propriétés
Abstraire des propriétés d’un objet, c’est les isoler du reste de l’objet et considérer qu’elles caractérisent une classe d’objets.
Cette forme d’abstraction est un processus cognitif élémentaire. En 1980, des scientifiques ont appris à des chimpanzés à distinguer des objets comestibles (bananes, pain, …) et des objets non comestibles (marteau, clous, …). Certains animaux sont donc capables d’abstraction !
Le processus d’abstraction peut être décomposé en trois étapes :
- Étape 1 : perception d’une qualité commune à différents objets.
Par exemple : j’observe qu’il y a des objets que je peux manger et d’autres que je ne peux pas manger - Étape 2 : création d’un terme qualifiant les objets de cette catégorie
Par exemple : Les objets que je peux manger seront qualifiés de « comestibles » - Étape 3 : création d’une propriété et d’une classe d’objetsOn crée par la même occasion une propriété : « être comestible » et la classe des objets qui possèdent cette propriété. Cette classe est « ouverte1» au sens que nous ne connaissons pas d’emblée tous les objets comestibles. Chaque fois qu’un objet se présentera à nous, nous déciderons s’il doit être ajouté ou non à cette classe.
Bien sûr les animaux se contentent de l’étape 1 et d’une version « inconsciente » de l’étape 3.
L’étape 2 nécessitant un langage évolué !
Ainsi lors des processus d’abstraction usuels, la donnée d’une propriété équivaut à la donnée d’une classe ouverte.
Création d’objets abstraits
Lorsque nous percevons que différents objets concrets ont des qualités communes, nous créons parfois un objet abstrait c’est-à-dire un type d’objets concrets. Nous appelons définition la liste des qualités nécessaires et suffisantes pour identifier le type d’un objet concret. Vérifier cette définition constitue une propriété d’un objet concret. Ainsi, comme précédemment, les objets concrets vérifiant cette définition constituent une classe ouverte.
Ainsi certaines des propriétés créées par l’abstraction ont ceci de particulier que la classe ouverte qui leur est associée a le statut d’objet abstrait. Ces propriétés sont appelées « définition d’un objet ».
Une orange, une chaise, une maison sont des objets abstraits.
On trouve dans un dictionnaire la définition de ces objets :
| Objet | Définition du dictionnaire |
| Une orange | Fruit comestible de l’oranger, d’un jaune tirant sur le rouge |
| Une chaise | Siège à pieds, à dossier, sans bras, pour une seule personne |
| Une maison | Bâtiment d’habitation |
Une orange peut être associée à la fois à une propriété ( « être un fruit comestible de l’oranger d’un jaune tirant sur le rouge » ) et à une classe ouverte (celle des fruits qui se présentent à nous et qui vérifient la définition d’une orange).
Remarquons la « circularité » de ces définitions qui font intervenir d’autres objets abstraits. On ne trouve pas dans un dictionnaire des définitions d’objets premiers à partir desquelles les autres objets seraient définis.
Il arrive parfois que le terme qualifiant les objets d’une catégorie devienne un objet abstrait immatériel. C’est le cas par exemple des couleurs. Définir une couleur particulière (le vert, le rouge …) simplement (sans faire intervenir la notion de longueur d’onde !) est impossible. C’est pourquoi les dictionnaires se contentent de citer des objets de cette couleur.
| Couleur | Définition du dictionnaire |
| Le rouge | Couleur du sang, du coquelicot, du rubis … |
| Le bleu | Couleur d’un ciel sans nuage, du bleuet, du saphir … |
| Le vert | Couleur des plantes à chlorophylle, d’une émeraude … |
En conclusion de ce premier paragraphe, nous pouvons dire que l’abstraction est le mécanisme qui nous permet d’acquérir une capacité à la généralisation. En passant d’un objet donné à une classe ouverte d’objets, nous passons du particulier au général.
II. LES CRÉATIONS DE L’ABSTRACTION MATHÉMATIQUE PRIMITIVE
Comme pour l’abstraction usuelle, l’abstraction mathématique crée des propriétés en 3 étapes.
Prenons l’exemple du nombre 5.
- Étape 1 : perception d’une qualité commune à différents objets.
J’observe qu’il y a un point commun entre l’ensemble des orteils d’un de mes pieds et l’ensemble des doigts d’une de mes mains. - Étape 2 : création d’un terme qualifiant les objets de cette catégorie.
En langue française cela correspond à la création de l’adjectif numéral « cinq » : mon pied a cinq orteils et ma main a cinq doigts. - Étape 3 : création d’une propriété et d’une classe d’objets.
Création de la propriété « être cinq » : qualité que l’on reconnaît dans tous les groupes de cinq objets.
Comme pour les couleurs, « cinq » devient un objet abstrait immatériel difficilement définissable autrement qu’en exhibant des exemples classiques de groupes de cinq objets. C’est ainsi que les dictionnaires définissent les nombres entiers :
| Nombre | Définition du dictionnaire |
| Cinq | Nombre de doigts dans une main, de branches à une étoile, de continents terrestres … |
| Sept | Nombre de jours de la semaine, de péchés capitaux … |
| Deux | Nombre des yeux d’un humain, de côtés d’une rue … |
Prenons maintenant l’exemple de la droite géométrique.
- Étape 1 : perception d’une qualité commune à différents objets.
J’observe qu’il y a une qualité commune à une corde tendue entre deux piquets, un rayon lumineux, un fil à plomb, le faite d’un toit, l’arête d’une règle, le trait que cette règle permet de tracer. - Étape 2 : création d’un terme qualifiant les objets de cette catégorie.
En langue française cela correspond à la création de l’adjectif « droit » : une corde tendue entre deux piquets, un rayon lumineux, un fil à plomb, le faite d’un toit, l’arête d’une règle, le trait que cette règle permet de tracer sont droits. - Étape 3 : création d’une propriété et d’une classe d’objets.
Création de la propriété « être droit » et de la classe des objets vérifiant cette propriété.
La propriété « être droit » devient un objet abstrait appelé « droite » comme la propriété « être un bâtiment d’habitation » devient un objet abstrait appelé « maison ».
Contrairement à un dictionnaire linguistique, le « dictionnaire mathématique » est construit sur des définitions d’objets premiers à partir desquelles les autres objets sont définis.
Par exemple, à partir des objets « droite » et « point », on peut définir les objets de la géométrie :
| Objet géométrique | Définition |
| Segment de droite | Portion d’une droite délimitée par deux points appelés extrémités |
| Polygone (éventuellement croisé) | Suite finie de points, dont le premier et le dernier sont confondus, et reliés par des segments de droite |
| Triangle | Polygone à trois côtés |
Nous voyons ainsi que les abstraits mathématiques primitifs sont semblables, quant à leur genèse, aux abstraits usuels. Afin d’augmenter le niveau de généralisation, nous verrons que les abstraits mathématiques primitifs vont subir deux nouveaux processus d’abstraction (l’idéalisation puis la formalisation), ce qui va conduire à diviser en trois sphères distinctes la connaissance mathématique.
III. LES TROIS SPHÈRES D’EXISTENCE DES ABSTRAITS MATHÉMATIQUES
La droite telle qu’elle nous est apparue dans le paragraphe précédent est celle que les enfants étudient à l’école primaire. Idéalisée, elle deviendra la droite étudiée dès le début du collège.
Le mathématicien russe Alexandre Danilovitch Alexandrov (1912 – 1999) écrit aux sujets des abstraits géométriques, dans son article « Vue d’ensemble des mathématiques » de l’ouvrage collectif Mathématiques, leur contenu, leurs méthodes, leur signification [1] paru en 1956 :
[…] une chose géométrique est avant tout une chose matérielle, considérée seulement du point de vue de sa forme spatiale, en faisant abstraction de ses autres propriétés comme sa densité, sa couleur, son odeur, son poids etc … Des propriétés d’un objet, la géométrie ne retient que sa forme et ses dimensions.
A vrai dire une figure géométrique peut être un concept encore plus général. On peut même faire abstraction de certaines extensions spatiales des objets à l’origine des concepts ; par exemple, une surface n’a que deux dimensions et une minceur infinie, une ligne n’a qu’une dimension, et un point aucune. Un point n’a pas de mesure.
ALEXANDROV, Alexandre D.
Mathématiques : Leur contenu, leurs méthodes, leur signification
Traducteur : CABANNES, André
Editions du Bec de l’Aigle, 2020
Volume 1 : 520 p. ISBN 9782957239122
Volume 2 : 678 P. ISBN 9782957239115
Volume 3 : 583 p. ISBN 9782957239139
Ainsi la notion de droite peut être d’abord conçue dans une première sphère de la connaissance mathématique que nous appellerons sphère sensible : C’est la sphère de la connaissance intuitive et expérimentale. Dans cette sphère, une droite est une ligne que l’on trace avec le crayon et la règle, et que l’on peut prolonger. Une telle ligne a une épaisseur (celle de la pointe du crayon) et ne peut être prolongée au-delà de la feuille de papier. Une telle droite est le produit de l’abstraction mathématique primitive évoquée au paragraphe II.
Pour gagner en précision et en généralité, le mathématicien souhaite poursuivre le processus d’épuration à partir du sensible et se débarrasser de certaines propriétés de l’objet jugées sources de complexification inutiles. Par exemple en enlevant à la droite son épaisseur on crée un objet plus simple mais complètement imaginaire. De même une droite ne peut être prolongée indéfiniment qu’en imagination. L’idéalisation des objets conduit par conséquent à une modification de la notion de vérité. A. D. Alexandrov écrit à ce sujet :
Du processus d’abstraction qu’opère la géométrie résulte sa nature spéculative. Avec des lignes droites sans épaisseur, avec de « pures formes », on ne peut plus faire d’expériences. On est réduit à raisonner, une conclusion atteinte servant de point de départ vers une suivante. C’est pourquoi les théorèmes de géométrie doivent être démontrés par des raisonnements, sinon ils n’appartiendraient pas à la géométrie, car ils ne concerneraient pas de « pures formes »
ALEXANDROV, Alexandre D.
Mathématiques : Leur contenu, leurs méthodes, leur signification
Cette droite sans épaisseur et indéfiniment prolongeable n’appartient plus à la sphère sensible mais à la sphère idéale.
Les nombres entiers, tels qu’ils nous sont apparus dans la sphère sensible au paragraphe précédent, vont également être idéalisés : la suite des nombres entiers peut être, en imagination, poursuivie sans interruption. A.D Alexandrov précise ce point :
Les grecs, au troisième siècle avant JC, comprirent […] que la suite des nombres entiers pouvait être continuée indéfiniment ; […] Du simple processus de comptage d’une collection d’objets, un par un, nous passons à l’idée d’un processus pour générer de manière illimitée en ajoutant chaque fois une nouvelle unité au dernier nombre qu’on a atteint. La série des nombres est maintenant perçue comme n’ayant pas de limite, et la notion d’infini entre en mathématiques. Évidemment, en pratique nous ne pouvons pas, en ajoutant constamment une nouvelle unité, aller jusqu’à n’importe quel nombre arbitraire. Qui peut compter jusqu’à un million de millions ? Même un siècle contient presque quatre cent fois moins de secondes. Mais là n’est pas la question. Le processus de formation d’une collection arbitrairement grande d’objets, n’a pas fondamentalement de limite. Par conséquent potentiellement – ou si l’on préfère dire, en théorie – on peut aller aussi loin que l’on veut sans jamais être bloqué. Les limitations pratiques du comptage n’ont aucune incidence sur le caractère infini de la suite de nombres. Dans la théorie ces limitations pratiques ne jouent aucun rôle
ALEXANDROV, Alexandre D.
Mathématiques : Leur contenu, leurs méthodes, leur signification
On observera que, dans l’idéalisation des abstraits primitifs de la géométrie et de l’arithmétique, l’infini fait son apparition au moins sous la forme d’une potentialité : la droite géométrique comme la suite des nombres entiers sont prolongeables autant que souhaité.
Ainsi avec les objets idéaux, on ne peut plus conduire des expériences comme avec les objets réels. Pour vérifier une assertion, il ne faut pas conduire une expérience mais mener un raisonnement.
C’est à la fois une nouvelle contrainte et une libération : le raisonnement permet de prévoir le résultat d’expériences impossibles à réaliser.
« Raisonner » consiste à établir la « vérité » ou la « fausseté » d’un énoncé portant sur des objets à partir d’énoncés dont la vérité est connue. Il est possible de raisonner à la fois dans la sphère sensible et dans la sphère idéale. Dans la sphère sensible on partira de vérités expérimentales et on obtiendra une vérité spéculative, qu’il sera ensuite possible de valider ou non par l’expérience. Dans la sphère idéale, il n’est pas possible de partir de vérités expérimentales, puisque les objets idéaux sont imaginaires. On comprend bien alors que cela nécessite de convenir d’un certain nombre de postulats. Si l’on veut être cohérent avec la nature du processus d’abstraction engagé, ces postulats devront pouvoir être interprétés dans la sphère sensible et correspondre à des vérités expérimentales. Autrement dit ces postulats ne sont pas des conventions arbitraires, ce sont des affirmations dont l’interprétation dans la sphère sensible est une évidence intuitive ou expérimentale.
Mais la notion d’évidence est une notion à la fois relative et subjective. Relative parce que dépendant des époques, des cultures … et subjective parce que ce qui est évident pour une personne ne l’est pas nécessairement pour une autre. Ainsi pour les mathématiciens grecs de l’Antiquité, il était évident que tous les nombres imaginables résultaient du partage d’un nombre entier par un autre nombre entier. Jusqu’au moment où ceux-ci parvinrent à démontrer que la longueur de la diagonale d’un carré de côté 1 ne pouvait s’écrire sous la forme d’une fraction … Si un postulat s’avère faux, c’est toute la théorie qui en découle qui s’écroule ! L’irrationalité de ![]() troubla tellement les pythagoriciens qu’ils cherchèrent d’abord à cacher ce résultat si dérangeant … Un postulat est parfois le résultat d’un consensus qui peut être soudainement brisé ! Le mathématicien suisse Ferdinand Gonseth (1890-1975) écrivait en 1936 dans son ouvrage Les mathématiques et la réalité
troubla tellement les pythagoriciens qu’ils cherchèrent d’abord à cacher ce résultat si dérangeant … Un postulat est parfois le résultat d’un consensus qui peut être soudainement brisé ! Le mathématicien suisse Ferdinand Gonseth (1890-1975) écrivait en 1936 dans son ouvrage Les mathématiques et la réalité
Il suffit de rappeler, par exemple, que le théorème de Bolzano : Toute courbe continue qui passe d’un point A situé au-dessus de l’axe des x à un second point B, situé au-dessous de cet axe, doit nécessairement couper ce dernier, a longtemps été considéré comme intuitivement évident. Le logicien Bolzano fut le premier à ressentir fortement la nécessité d’une démonstration, qui rattachât plus étroitement l’énoncé aux prémisses et spécialement à la définition de la courbe continue. Dans un ordre d’idées assez semblable, il fallut attendre jusqu’à Dedekind pour que fût donnée la définition actuellement acceptée du nombre irrationnel et du continu des nombres… et pourtant l’on ne s’est pas fait faute de s’en servir avant lui. Dans ses recherches de géométrie, Poncelet faisait couramment appel à son fameux principe de continuité qu’aucun mathématicien ne se permettrait plus d’invoquer sans le justifier, etc.
Il faut en prendre son parti : le sentiment de l’évidence varie avec les époques. L’étudiant d’aujourd’hui apprend à rejeter, comme insuffisamment fondé, tel raisonnement sur lequel Euler n’hésitait pas à s’appuyer : mais sans que le mathématicien d’aujourd’hui ait une vue plus claire des sources de l’évidence en elle-même que ne l’avait le mathématicien d’hier ou d’autrefois.
GONSETH, Ferdinand.
Les mathématiques et la réalité : Essai sur la méthode axiomatique
Albert Blanchard, 2000. 386 p. ISBN 978285367112
D’autre part, les postulats sont des énoncés qui concernent des objets idéaux premiers c’est-à-dire à partir desquels tous les autres objets idéaux sont construits.
Or il s’avère que définir ces objets premiers est impossible ! Dans la définition usuelle d’une « droite » nous avons besoin de la notion de « point » : « Une droite est un objet formé de points alignés. Elle est illimitée et sans épaisseur ». Dans la définition usuelle d’un « point » nous avons besoin de la notion de « droite » : « un point est l’unique objet commun à deux droites sécantes. » Les objets premiers sont en réalité indéfinissables ! Construire une théorie mathématique sur des vérités relatives et subjectives portant sur des objets indéfinissables : cela ne semble guère satisfaisant (même si les mathématiciens s’en contentèrent jusqu’au XIX° siècle …).
Face à ces écueils, certains mathématiciens du XIX° siècle prennent la décision radicale de cesser de prendre en considération la nature des objets premiers manipulés pour se concentrer uniquement sur les relations qui existent entre eux. Contrairement à la nature des objets premiers (qui semble en définitive insaisissable), le système de relations qui existe entre les objets premiers semble plus facile à cerner.
Parmi ces mathématiciens, il convient de citer Giuseppe Peano (1858 – 1932) qui proposa en 1889 une axiomatisation de l’arithmétique des entiers naturels et David Hilbert (1862 – 1943) qui proposa en 1899 une axiomatisation de la géométrie euclidienne (ce sont les travaux de Peano qui ont inspiré Hilbert).
Plutôt que de chercher à définir individuellement les objets idéaux premiers que sont la droite et le point, le mathématicien David Hilbert a cherché à exprimer toutes les relations liant le point et la droite :
- Par deux points distincts, passe une seule droite.
- Sur une droite sont situés au moins deux points, et pour une droite donnée, il existe au moins un point qui n’est pas sur la droite.
- Par un point A non situé sur une droite d passe une seule droite d’ n’ayant aucun point commun avec d.
Ces trois relations ne définissent pas le point et la droite mais expriment toutes les relations qui les unissent. Les relations 1), 2) et 3) sont appelés des axiomes.
Remarquons que notre objet idéal « droite du plan » que nous avions esquissé de manière subjective n’est pas le seul à vérifier ces trois relations.
Imaginons un « plan » formé de neuf points disposés ainsi :
![Rendered by QuickLaTeX.com \[\begin{array}{crcrc} A\times&& B \times &&C \times \\&&&&\\D \times&& E \times && F \times \\&&&&\\G \times& &H \times && I\times \\\end{array}\]](https://wp.u-picardie.fr/irem/wp-content/ql-cache/quicklatex.com-28f0978c3d50418d2757823d77d3221a_l3.png)
Dans ce plan, je décide d’appeler « droite » chacun des 12 ensembles
Les points et les droites de ce « plan » vérifient les 3 axiomes précédents.
A chacun des deux mots « point » et « droite », nous pouvons associer des objets idéaux (ou sensibles) de différente nature qui vérifieront nos axiomes. Ces deux mots sont donc en quelque sorte des « coquilles vides » c’est-à-dire des « formes » susceptibles d’accueillir différents contenus.
Nous avons donc quitté la sphère idéale pour une nouvelle sphère de la connaissance mathématique : la sphère formelle. Les objets formels sont susceptibles d’être interprétés diversement dans la sphère idéale ou dans la sphère sensible. Les axiomes ne définissent pas (complètement) les objets formels ! Ainsi lors du processus d’abstraction, nous voyons que l’objet réel en s’idéalisant puis en se formalisant a perdu sa substance. La seule qualité qu’il reste à l’objet formel est celle d’entrer en relation avec d’autres objets. L’objet formel n’a plus d’objet que le nom : il est devenu un « simple nœud logique ».
Nous voyons également que la sphère idéale a un double visage : elle est l’abstrait de la sphère sensible et le concret de la sphère formelle. Il est important de comprendre que les trois sphères (sensibles, idéales et formelles) coexistent et ne se « supplantent » pas, comme l’explique très bien Ferdinand Gonseth :
Insistons d’abord sur le fait qu’un concept n’a pas une forme donnée une fois pour toutes et un contenu ne varietur. Ainsi la notion de droite nous est apparue trois fois sous des aspects de plus en plus dépouillés : une première fois comme représentation intuitive accessible même à l’esprit resté vierge de culture mathématique et telle que l’évoquent les expressions : « droit devant soi » ou « sans incliner ni à droite ni à gauche ». Le second avatar peut être placé sous le signe de la géométrie grecque, tandis que le troisième est celui de la relation logique. Il n’est pas vrai que le dernier remplace les précédents et les détruise. Il ne peut exister sans eux, sans y fonder son sens, sans en recevoir sa substance.
Au contraire, même après avoir pris sa forme la plus épurée, le concept droite continue à vivre parallèlement de ses existences antérieures. Il se fait une espèce de projection des plans d’existence l’un sur l’autre, sans que ni l’un ni l’autre ne renonce à son rôle. Le concept comprend à la fois l’amalgame et la dissociation de ses trois formes
GONSETH, Ferdinand.
Les mathématiques et la réalité : Essai sur la méthode axiomatique
Albert Blanchard, 2000. 386 p. ISBN 9782853671125
IV. THÉORIES MATHÉMATIQUES
La trichotomie sensible/idéale/formelle de la connaissance mathématique correspond à son développement historique (jusqu’au VII° siècle avant JC / du VII° siècle avant JC jusqu’au XIX° siècle / du XIX° siècle à aujourd’hui) et également à l’organisation chronologique de son enseignement (primaire /secondaire / supérieur).
Une théorie, nous dit le Petit Robert, est un ensemble d’idées, de concepts abstraits, plus ou moins organisés appliqué à un domaine particulier. Nous avons vu que les premiers abstraits mathématiques « habitent » la sphère sensible : les figures géométriques tracées avec la règle et le compas, les nombres entiers vus comme propriété quantitative d’un groupe d’objets sont des abstraits sensibles. On peut donc parler de théorie mathématique dans la sphère sensible. Cependant les mathématiques ne s’y présentent pas vraiment comme une théorie déductive mais plutôt comme une compilation de constatations expérimentales. Voici ce qu’écrit A.D Alexandrov à ce sujet :
Les Egyptiens et les Babyloniens furent capables de déterminer les surfaces et les volumes les plus simples. Ils connaissaient avec une précision raisonnable le ratio entre la circonférence du cercle et son diamètre ; il est même possible qu’ils aient su calculer la surface d’une boule. En un mot, ils avaient déjà des connaissances géométriques impressionnantes. Néanmoins, pour autant que l’on sache, ils ne concevaient pas encore la géométrie comme une science théorique avec des théorèmes et des démonstrations. De même que l’arithmétique de leur temps, la géométrie était pour eux essentiellement une collection de règles dérivées de l’expérience. En outre, la géométrie n’était pas du tout séparée de l’arithmétique. Les problèmes de géométrie étaient simultanément des problèmes d’arithmétique où il fallait calculer des choses.
ALEXANDROV, Alexandre D.
Mathématiques : Leur contenu, leurs méthodes, leur signification
La notion de théorie mathématique déductive ne trouve pleinement son sens que dans la sphère idéale ou dans la sphère formelle. Dans la sphère idéale une théorie est la donnée de
- définitions d’objets premiers et de postulats les concernant ;
- de définitions d’objets secondaires et de théorèmes les concernant déduits des postulats.
Dans la sphère formelle une théorie est la donnée
- d’axiomes c’est-à-dire des énoncés affirmables librement par convention ;
- de théorèmes déduits des axiomes.
Dans une théorie formelle, la notion de définition n’est pas nécessaire puisqu’en définitive on ne manipule que des symboles. Une définition n’est donc dans la sphère formelle, qu’une simple convention pour une notation, dont le but est de simplifier la lecture des énoncés de cette théorie.
On notera que dans cet exposé on appelle postulats les « axiomes idéaux » et axiomes les « axiomes formels ».
V. LA NOTION DE VÉRITÉ EN MATHÉMATIQUES
Dans la sphère sensible, la notion de vérité se rapporte à des faits concernant des objets réels. C’est une vérité perçue, expérimentée. Sa validité est relative à la précision de nos sens ou de nos instruments de mesure. Pour reprendre une expression de Ferdinand Gonseth, cette vérité est valide « tant que nous n’en forçons pas la portée ». Ferdinand Gonseth proposede définir le vrai de la sphère sensible
comme étant ce qui ne peut être démenti par les événements ou les faits… Mais à condition que la vérification dépende elle-même d’une action simple, ou d’une constatation de sens commun. « Est-il vrai, oui ou non, que la neige soit blanche ? » — « Mais certainement, à la condition que vous fassiez abstraction de cette ombre bleue, de ce reflet jaunâtre, de cette bande grise, etc. Ne vous arrêtez pas trop aux détails, sans quoi il nous faudra analyser toutes les circonstances, et appeler tous les ordres de la connaissance à notre secours. Acceptez la définition précédente pour ce qu’elle vaut : nous savons bien combien elle est sommaire, et que tous les termes en deviennent problématiques si l’on en veut serrer le sens de trop près
GONSETH, Ferdinand.
Les mathématiques et la réalité : Essai sur la méthode axiomatique
Dans la sphère idéale, la notion de vérité se rapporte à des objets imaginaires. La « vérité idéale » est donc elle aussi … imaginaire ! Elle est déduite de celle des postulats, qui provient de « vérités sensibles idéalisées ». Nous avons vu que la vérité de ces postulats est subjective. Les vérités de la sphère idéale ne sont pas (réellement) absolues ! Une question naturelle qui se pose de plus est : les vérités idéales déduites des postulats peuvent-elles être toujours interprétées par des vérités dans la sphère sensible ?
En effet si les postulats peuvent s’interpréter comme des évidences dans la sphère sensible, la sphère idéale a sa propre autonomie. Ses théorèmes concernent des objets idéaux.
Voici ce qu’en disait le mathématicien russe Vladimir Igorevitch Arnold (1937 – 2010) dans son article Sur l’éducation mathématique paru en 1998 dans la gazette de la SMF (Le terme axiome est ici utilisé dans le sens « d’axiome idéal », c’est-à-dire (avec la terminologie utilisée dans cet exposé) dans le sens de « postulat ») :
En mathématique a été mise au point une technique particulière qui peut parfois être utile pour les applications pratiques mais qui peut nous induire en erreur. Elle s’appelle la modélisation. Pour la construction d’un modèle on fait l’idéalisation suivante : certains faits, connus seulement avec un certain degré d’approximation ou de probabilité, sont considérés comme absolument vrais et sont pris comme « axiomes ». La signification de cet « absolu » est exactement que nous nous permettons d’agir avec ces « faits » selon les règles de la logique formelle, en appelant « Théorèmes » les déductions que nous en tirons. Il est clair que dans aucune action réelle on ne peut s’appuyer entièrement sur de telles déductions, parce que les paramètres des phénomènes étudiés ne sont pas connus tout à fait exactement, et qu’une petite modification (par exemple des conditions initiales du processus) peut complètement bouleverser le résultat. C’est ainsi qu’il n’est pas possible d’espérer des prévisions météorologiques dynamiques sur une longue période, et que cela restera impossible quels que soient les perfectionnements des ordinateurs et de l’enregistrement des données. De même une petite modification des axiomes (en lesquels de toute façon nous ne pouvons avoir totalement confiance) peut conduire à d’autres conclusions que celles fournies par les théorèmes obtenus. Plus sont longs et astucieux les raisonnements (« démonstrations »), moins le résultat final est robuste. Les modèles compliqués sont rarement utiles (sauf pour écrire des thèses). La technique mathématique de modélisation consiste en ce qu’on oublie les défauts et on parle des modèles déductifs comme s’ils coïncidaient avec la réalité. Le fait même que cette méthode évidemment incorrecte du point de vue scientifique conduise souvent à des résultats utiles est appelé « l’efficacité déraisonnable des mathématiques dans les sciences physiques » (Wigner).
Ainsi les vérités déduites des postulats idéaux ne coïncident pas nécessairement avec des vérités de la sphère sensible. Cette coïncidence n’est jamais « garantie » : seule une constatation expérimentale peut valider cette coïncidence. La « foi » dans une théorie idéale est d’autant plus grande que les validations expérimentales des théorèmes sont nombreuses. Le jour où un théorème se trouve invalidé par l’expérience, la foi dans la théorie décline ou le champ d’application de cette théorie se rétrécit.
Dans la sphère formelle les axiomes portent sur des objets formels dont nous avons vu qu’ils sont de simples nœuds logiques. La vérité des axiomes est donc purement conventionnelle. Il n’est en effet a priori pas nécessaire que ceux-ci s’interprètent comme des vérités dans la sphère sensible. On peut donc imaginer une théorie formelle basée sur des axiomes qui contredisent l’intuition sensible ou qui n’ont pas de lien avec elle. Dans ces conditions dire qu’un théorème d’une théorie formelle est « vrai » signifie simplement qu’il est « prouvable » c’est-à-dire « déductible des axiomes ». Albert Einstein (1879-1955) écrivait en 1916 dans son ouvrage La relativité :
La géométrie part de certaines notions fondamentales telles que le point, la droite, le plan, auxquelles nous sommes capables d’associer des représentations plus ou moins claires, et de certaines propositions simples (axiomes), que nous sommes disposés à regarder, en vertu de ces représentations, comme « vraies ».
Toutes les autres propositions sont ensuite ramenées, au moyen d’une méthode logique dont nous nous sentons forcés de reconnaître la légitimité, aux axiomes, c’est-à-dire démontrées. Une proposition est, par conséquent, exacte ou « vraie », si elle est déduite des axiomes de la manière généralement admise. La question de savoir si telle ou telle proposition géométrique est « vraie » se ramène, par conséquent, à la question de savoir si les axiomes sont « vrais ».
Mais on sait depuis longtemps que non seulement on ne peut répondre à cette dernière question au moyen des méthodes de la géométrie, mais qu’elle n’a en elle-même aucun sens. On ne peut pas demander s’il est vrai que par deux points il ne passe qu’une seule droite. On peut seulement dire que la Géométrie euclidienne traite de figures qu’elle appelle « droites » et auxquelles elle attribue la propriété d’être déterminées d’une manière univoque par deux de ses points. La notion de « vrai » ne s’applique pas aux énoncés de la géométrie pure, car par le terme « vrai » nous désignons, en dernier ressort, toujours la concordance avec un objet « réel ». Or, la Géométrie ne s’occupe pas du rapport entre ses notions et les objets de l’expérience, mais seulement du rapport logique de ces notions entre elles.
EINSTEIN, Albert.
La relativité
Traducteur : SOLOVINE, Maurice
Payot, 1990. 240 p. ISBN 9782228882545
Un exemple de théorie formelle dont un axiome contredit l’intuition sensible est la géométrie hyperbolique imaginée en 1837 par le mathématicien russe Nikolaï Ivanovitch Lobatchevski (1792 – 1856). Comme cette géométrie possède un axiome contrariant l’intuition sensible : « Par un point extérieur à une droite passent une infinité de droites parallèles à celle-ci », il appela cette géométrie « géométrie imaginaire ». Notons que cette géométrie étant antérieure aux travaux de Hilbert sur l’axiomatisation, elle ne fut pas exposée par Lobatchevski sous la forme d’une théorie formelle mais sous la forme d’une théorie idéale (dont un des postulats n’était pas évident !).
V.I. Arnold nous a expliqué que, dans la sphère idéale, même en partant de postulats interprétables en énoncés « vrais » de la sphère sensible, les énoncés « idéalement vrais » que nous pouvions en déduire n’étaient pas nécessairement interprétables en énoncés « vrais » dans la sphère sensible. Si nous partons d’axiomes formels dont l’interprétation sensible est contradictoire ou sans lien avec les vérités de la sphère sensible, la question de la vérité des interprétations sensibles des théorèmes déduits des axiomes formels ne se pose pas. Mais alors à l’aune de quel critère allons-nous juger un système d’axiomes ?
Ce que le mathématicien attend en premier lieu d’un système d’axiomes est qu’il soit non-contradictoire, c’est-à-dire qu’il ne soit pas possible au moyen d’un raisonnement considéré comme « valide » de prouver et de réfuter un même énoncé. Selon Ferdinand Gonseth, ce que le mathématicien exige
des axiomes et de leurs conséquences, c’est que jamais leur ensemble ne contienne deux propositions incompatibles. [Il n’exige] pas qu’une proposition isolée ni qu’un axiome déterminé soit vrai en soi : [Il se contente] de l’absence de contradiction. [Sa] doctrine, plutôt que de l’idéal d’une vérité absolue, s’inspire de la règle de conduite que voici : « Toute construction intellectuelle peut être tenue pour vraie tant qu’elle échappe à la contradiction. »
[…] l’intervention du non-contradictoire en lieu et place du vrai totalitaire n’est pas l’effet du hasard, mais d’un événement mathématique de toute importance : de la découverte des géométries non-euclidiennes. Pour Euclide et ses prédécesseurs, l’idée du vrai géométrique était étroitement associée à celle de l’adéquation au réel. Le réel physique était, il est vrai, regardé comme fortuit et imparfait, et ne correspondant que d’assez loin à l’idéal de la forme géométrique. Celle-ci, dans sa vérité univoque, devait cependant rester discernable dans l’imperfection de ses réalisations. Cette notion fort complexe devait rester encore longtemps intacte.[…] Il est dès lors tout à fait clair que les systèmes d’axiomes qu’on a le droit de « tenir pour vrais » ne sont pas ceux qui sont aperçus comme vrais du fait d’une évidence toute spéciale, mais simplement ceux qui n’impliquent pas contradiction. Le fléchissement de la notion primitive de vérité me paraît absolument indéniable.
GONSETH, Ferdinand.
Les mathématiques et la réalité : Essai sur la méthode axiomatique
Dans la sphère formelle, il est donc indispensable de pouvoir déterminer si un système d’axiomes est ou n’est pas contradictoire. On dit qu’une théorie formelle est consistante ou cohérente si sa base axiomatique est non-contradictoire. Comment savoir si c’est effectivement le cas ? Hilbert pense qu’il est possible de répondre à cette question et lance en 1920 un programme de recherche. Hilbert pense même que toutes les mathématiques découlent d’un nombre fini d’axiomes dont on pourrait montrer qu’ils forment un système cohérent. Mais en 1931, le mathématicien autrichien Kurt Gödel (1906 – 1978) démontre que les systèmes d’axiomes utilisés pour formaliser tout ou partie des mathématiques usuelles ne peuvent démontrer leur propre cohérence. Le programme de Hilbert n’est donc pas (pleinement) réalisable !
VI. LE RAISONNEMENT MATHÉMATIQUE
Dans la sphère sensible le raisonnement se réduit à des évidences, des corrélations et des causalités validées par l’expérience. Là encore citons Ferdinand Gonseth (ce que Gonseth désigne par sphère intuitive correspond à ce que cet exposé désigne par sphère sensible) :
Dans les expressions que voici :
GONSETH, Ferdinand.
Si je sais que le soleil luit, j’en déduis qu’il fait jour.
Si nous jouons à deux et si je perds, il faut bien que tu gagnes.
Si nous marchons côte à côte et si tu n’es pas à ma droite, je sais en inférer que tu es à ma gauche.
S’il y a moins de deux personnes à m’attendre, j’en déduis qu’il n’y en a qu’une ou que personne ne m’attend,
le fait de conséquence est l’expression directe de réalités liées dans la connaissance intuitive que nous en possédons. Les deux premières font surtout appel à une relation de causalité, la troisième à l’intuition de l’espace, la dernière à l’intuition du nombre. Peut-on parler ici de déduction logique ?
[…] Le caractère logique s’introduit ici du fait que l’on porte l’accent sur l’opération intellectuelle qui établit la relation, sur l’association des idées. En disant « logique », on évoque simplement une certaine autonomie du jugement alliée à une évidente efficacité. C’est cette logique qui fait le fond de ce qu’on appelle la « saine raison ». À ce niveau, on raisonne sainement si l’on fait des associations d’idées correctes ; mais cette correction est en fonction de la conformité au réel des vues qui président à l’association des idées.
Ainsi l’on voit que la notion de déduction existe déjà dans ce que nous avons nommé la sphère intuitive, mais qu’elle est encore loin de répondre à l’idéal de la déduction proprement dite. Nous parvenons à cette dernière à partir de la première, dans toutes ses variétés, par schématisation et abstraction.
Permettez-que j’y insiste : de même que la notion de la droite géométrique est le fait d’un acte intellectuel créateur qui s’exerce sur ce que, après coup, nous nommons les réalisations de la droite, la notion de déduction pure est l’aboutissement d’un processus de schématisation qui s’opère sur l’ensemble de nos « raisonnements intuitifs » efficaces, sur toutes les associations d’images mentales où, après coup, nous pouvons apercevoir la forme de la déduction logique.
Les mathématiques et la réalité : Essai sur la méthode axiomatique
Ainsi dans la sphère sensible nos déductions sont des associations d’idées que nous estimons valides parce que conformes à ce que nous avons « l’habitude » de constater.
Le philosophe David Hume (1711 – 1776) écrivait en 1748 dans Enquête sur l’entendement humain [4] :
Quand un objet ou un événement naturel se présente, il nous est impossible, quelle que soit notre sagacité ou notre pénétration, de découvrir ou même de conjecturer sans expérience quel événement en résultera […] Même après un seul cas ou une seule expérience, où nous avons observé qu’un événement particulier s’ensuivait d’un autre, nous ne sommes pas autorisés à former une règle générale […] Mais lorsqu’une espèce particulière d’événement a toujours été, dans tous les cas, jointe à une autre, nous ne faisons plus dorénavant aucun scrupule de prédire l’un d’après l’apparition de l’autre […] Il apparaît donc que cette idée d’une connexion nécessaire entre des événements provient d’une pluralité de cas semblables qui se présentent, de constante jonction entre ces événements ; et cette idée ne saurait jamais être suggérée par aucun de ces cas en particulier, examiné sous tous les points de vue et dans toutes les positions possibles. Mais il n’y a rien dans une pluralité de cas, qui diffère de chacun des cas particuliers, qu’on suppose exactement semblables ; excepté seulement qu’après une répétition de cas semblables, l’esprit est porté par habitude, lorsque apparaît l’un des événements, à attendre son concomitant ordinaire, et à croire qu’il existera. Cette connexion que nous sentons dans l’esprit, cette transition habituelle de l’imagination de l’un des objets à son concomitant ordinaire, tel est donc le sentiment ou l’impression d’où nous formons l’idée de force ou de connexion nécessaire.
HUME, David.
Enquête sur l’entendement humain.
Traducteur : MALHERBE, Michel
Vrin, 2008. 420 p. ISBN 9782711619900
Dans la sphère idéale, les déductions demeurent des corrélations motivées par la sphère sensible. Certes elles portent sur des objets imaginaires mais ceux-ci schématisent des objets réels. Les corrélations « perçues » sur les objets idéaux trouvent leurs origines dans les habitudes « contractées » dans la sphère sensible. Dans la sphère formelle, nous ne disposons pas de corrélations conformes au réel. La notion de vérité disparait. L’acte déductif doit donc lui aussi être formalisé !
Dans la citation d’Albert Einstein évoquée précédemment, celui-ci écrit : « Une proposition est, par conséquent, exacte ou « vraie », si elle est déduite des axiomes de la manière généralement admise »
Que veut dire Albert Einstein lorsqu’il évoque une manière généralement admise de raisonner ?
Comment décidons-nous dans la sphère formelle qu’un raisonnement est ou n’est pas valide ?
Cette décision dépend de la « forme » de celui-ci et non de la vérité des affirmations qui le composent.
Par exemple, le syllogisme :
Tous les objets rares sont chers
Tous les objets bon marché sont rares
Donc tous les objets bon marché sont chers
est valide bien que sa conclusion ne soit pas vraie (dans la sphère sensible).
Il est valide parce qu’il est de la forme :
Tous les A sont B
Tous les B sont C
donc tous les A sont C
Mais pourquoi cette forme est-elle valide ? Parce qu’à chaque fois que l’on « remplace » A, B et C par des objets de la sphère sensible tels que « Tous les A sont B » et « Tous les B sont C » soient des énoncés vrais (dans la sphère sensible), on obtient toujours que « Tous les A sont C » est également un énoncé vrai (dans la sphère sensible).
Le syllogisme précédent a une conclusion fausse car la deuxième prémisse introduit une équivoque sur le mot « rare » : c’est le fait d’être bon marché qui est rare et non l’objet. La deuxième prémisse doit donc être considérée comme fausse, d’où la nature sophistique de ce syllogisme.
Plus généralement, un raisonnement est valide si chaque fois qu’il est instancié dans la sphère sensible, on obtient du vrai sensible à partir du vrai sensible. Il faudra là encore poser des conventions : de même qu’il a fallu choisir les vérités premières, il faut choisir les raisonnements valides. Ces conventions seront motivées par la sphère sensible : telle forme de raisonnement est valide parce que dans de nombreuses situations de la sphère sensible où il est appliqué, on obtient du vrai et jamais du faux, à partir du vrai. Dans la logique moderne, la recherche des raisonnements valides ne passe pas par la recherche des syllogismes valides comme le faisait Aristote dans son Organon mais commence par une formalisation du langage avec notamment l’utilisation de symboles de connecteurs et de quantificateurs.
Dans la sphère formelle, un énoncé déductible des axiomes, au moyen d’un (ou plusieurs) raisonnement(s) valide(s) (successifs) ou d’aucun, est dit prouvable. Les axiomes d’une théorie formelle sont donc prouvables (par définition de la prouvabilité).
Mais il existe des énoncés qui sont prouvables sans être réellement déduits des axiomes au sens où ils peuvent être déduits de n’importe quel énoncé (prouvable ou non). Leur prouvabilité ne dépend pas de leur contenu mais de leur forme. Envisageons par exemple l’énoncé : « Si A est B alors A est B ». Si l’on interprète A et B par des objets de la sphère sensible, cet énoncé sera toujours vrai. Dans la sphère formelle, il faudra donc être capable de déterminer les formes d’énoncés dont les interprétations sensibles sont toujours vraies.
De tels énoncés sont dits tautologiques. Il faudra également être capable de déterminer les formes d’énoncés dont les interprétations sensibles sont toujours fausses. De tels énoncés sont dits antilogiques.
Les énoncés tautologiques et antilogiques, tout comme les axiomes d’une théorie, sont la conséquence d’un choix motivé par la sphère sensible. Il existe donc plusieurs façons de procéder ! Les lois de la logique ne sont pas gravées dans le marbre ! Comme l’explique plus haut Ferdinand Gonseth, l’acte déductif existe dans la sphère sensible. C’est dans cette activité déductive primitive (qui est celle des enfants qui raisonnent sans se référer consciemment à des formes logiques) que sont observées des similitudes (et donc des formes). Les formes observées dépendent de la subjectivité de l’observateur … C’est pourquoi il existe diverses logiques formelles : logique classique, logique intuitionniste, logique modale …
Les énoncés tautologiques sont appelés axiomes logiques et les axiomes propres à la théorie sont appelés axiomes spécifiques.
Appelons négation d’un énoncé formel A le symbole Non(A). En logique classique, on décide que si A est tautologique alors Non(A) est antilogique et que si A est antilogique alors Non(A) est tautologique.
Un énoncé formel A est dit réfutable si Non(A) est prouvable.
Contrairement aux sphères sensibles et idéales, où un énoncé est vrai ou faux, il y a donc a priori quatre alternatives pour un énoncé formel. Il peut être :
- prouvable et non réfutable ;
- réfutable et non prouvable ;
- ni prouvable ni réfutable ;
- prouvable et réfutable.
Si une théorie comporte des énoncés à la fois prouvables et réfutables (un tel énoncé est dit contradictoire) cela signifie que la base axiomatique est incohérente. Un énoncé qui n’est ni prouvable ni réfutable est dit indécidable. Ainsi dans le cadre d’une théorie cohérente dont le système déductif est la logique classique, il reste trois alternatives : un énoncé formel est soit prouvable, soit réfutable, soit indécidable. Notons que l’existence d’énoncés indécidables dans le cadre d’une théorie formelle cohérente, dont on sait exhiber (algorithmiquement) un système d’axiomes parmi les énoncés prouvables et suffisamment évoluée pour formaliser l’arithmétique de Peano, a été établie par Kurt Gödel en 1931.
Un énoncé indécidable d’une théorie (ou la négation de celui-ci) peut être ajouté au système axiomatique de cette théorie. On obtient alors une nouvelle théorie qui « complète » la première. Cette complétion n’est que partielle : la nouvelle théorie obtenue comporte elle-aussi des énoncés indécidables.
La décision d’ajouter ou non un énoncé indécidable à la base axiomatique d’une théorie relève d’un choix qui peut avoir diverses motivations subjectives (car relatives à des implicites de la sphère idéale que l’on souhaite « capter »).
VII. MODÈLES D’UNE THÉORIE FORMELLE
Parmi les axiomes de la géométrie euclidienne, le postulat « Par un point A non situé sur une droite d passe une seule droite d’ n’ayant aucun point commun avec d » est un peu particulier car il est impossible à vérifier dans la sphère sensible. Pour vérifier expérimentalement que deux droites ne se coupent pas, il faudrait comme l’écrit A.D Alexandrov « les parcourir dans les deux directions « jusqu’à l’infini » et vérifier qu’elles n’ont pas d’intersection où que ce soit sur une étendue infinie. »
C’est pourquoi les grecs cherchèrent à se passer de ce postulat, appelé « cinquième postulat ». De nombreux mathématiciens par la suite ont essayé de démontrer qu’il était une conséquence des autres postulats. Toutes ces tentatives ont échoué et la solution à ce problème fut trouvée par Lobatchevski. En 1835, dans un essai intitulé Nouveaux Principes de Géométrie, il explique que toutes les vaines tentatives pour démontrer ce postulat l’ont « amené à suspecter que les concepts eux-mêmes ne contiennent pas la vérité qu’on a cherché à démontrer et, comme les autres lois de la physique, qu’ils peuvent seulement être vérifiées par l’expérience, c’est-à-dire par exemple par des observations astronomiques ». En supposant que la négation de ce postulat était vraie, Lobatchevski essaya en vain d’arriver à une contradiction. Il fit alors deux hypothèses :
- Le cinquième postulat n’est pas une conséquence des autres postulats.
- En partant de la négation du cinquième postulat, on peut comme l’écrit A.D Alexandrov « développer toute une chaîne de conséquences ».
La négation du cinquième postulat est « Par un point A non situé sur une droite d, ou bien il passe au moins deux droites n’ayant aucun point commun avec d ou bien il ne passe aucune droite n’ayant aucun point commun avec d ». Lobatchevski choisit l’énoncé « Par un point A non situé sur une droite d, il passe au moins deux droites n’ayant aucun point commun avec d » pour remplacer le cinquième postulat et en déduire une géométrie non euclidienne appelée géométrie hyperbolique. L’autre possibilité, c’est-à-dire le choix de l’énoncé « Par un point A non situé sur une droite d, il ne passe aucune droite n’ayant aucun point commun avec d », conduit à une autre géométrie non euclidienne appelée géométrie elliptique.
Comme l’explique A.D Alexandrov, la géométrie hyperbolique fut développée par Lobatchevski
comme une géométrie concevable ou envisageable, comme un ensemble de théorèmes pouvant être démontrés logiquement : c’est-à-dire qu’ils sont les conséquences logiques de cette hypothèse, à laquelle on a adjoint les autres hypothèses de la géométrie euclidienne, que Lobatchevski appelle la géométrie ordinaire […] Cependant, tous les raisonnements et conclusions [obtenus] demeuraient en quelque sorte, seulement des jeux de l’esprit. Ils restaient en outre assez difficiles à suivre tant que le sens simple et réel de la géométrie de Lobatchevski au sein du système familier des concepts de la géométrie euclidienne n’avait pas été dégagé.
ALEXANDROV, Alexandre D.
Mathématiques : Leur contenu, leurs méthodes, leur signification
En effet comment être sûr dans une telle démarche spéculative qu’une contradiction n’arrivera jamais ? A quoi bon construire une théorie qui ne « correspond » à rien de réel ? Une réponse satisfaisante à ces questions fut apportée en 1870 par le mathématicien allemand Félix Klein (1849 – 1925).
Il propose ce que l’on appelle une représentation (ou une réalisation) idéale de la géométrie imaginée par Lobatchevski. Pour cela il fait correspondre (dans la sphère idéale) à chacun des objets de la géométrie de Lobatchevski des objets de la géométrie euclidienne :
- Au « plan » de Lobatchevski, il associe un disque du plan euclidien sans sa frontière ni ce qui est à l’extérieur.
- Aux « droites » de Lobatchevski, il associe les cordes du disque (sans leurs extrémités).
Grâce à d’autres correspondances que nous ne détaillerons pas ici, A.D Alexandrov explique qu’
il s’avère que tous les faits de la géométrie ordinaire à l’intérieur du disque ont pour homologues des théorèmes de la géométrie de Lobatchevski, et vice versa : la géométrie de Lobatchevski est interprétée (modélisée) à l’aide de la géométrie ordinaire à l’intérieur d’un disque […] Quand ce modèle de la géométrie de Lobatchevski a été présenté, cela montra que cette géométrie avait une signification réelle et simple. La géométrie de Lobatchevski est vraie car elle peut être vue comme une interprétation particulière de la géométrie ordinaire sur un disque. Cela démontra qu’elle était cohérente : ses conclusions ne peuvent en effet pas davantage conduire à une contradiction que les axiomes de la géométrie euclidienne ordinaire, puisque n’importe quelle conclusion de la géométrie de Lobatchevski peut être traduite dans le langage de la géométrie euclidienne ordinaire sur un disque. Les mathématiciens ont l’habitude de dire que la géométrie de Lobatchevski a une représentation dans la géométrie euclidienne, et par conséquent est cohérente dans la même mesure où l’est la géométrie euclidienne
ALEXANDROV, Alexandre D.
Mathématiques : Leur contenu, leurs méthodes, leur signification
La notion de « représentation » ou de « réalisation » ou de « modèle » à l’époque de Félix Klein permet de « plonger » une théorie T dans une théorie T’ en identifiant (de manière biunivoque) chacun des objets de T à un objet de T’ et chacune des relations entre objets de T à une relation entre les objets correspondants de T’ dans la sphère idéale.
Mais comment démontrer rigoureusement que le modèle de Klein interprète correctement la géométrie hyperbolique dans la géométrie euclidienne ? Cela ne fut possible que trente ans après les travaux de Félix Klein, grâce à l’axiomatisation formelle de la géométrie euclidienne par David Hilbert. En effet comme les raisonnements formellement valides ont pour propriété espérée de produire du « vrai sensible » à partir du « vrai sensible », A.D Alexandrov écrit
qu’il serait oiseux en effet de vérifier les théorèmes de Lobatchevski les uns après les autres ; ils sont nombreux, et même en réalité en nombre infini puisqu’on peut toujours en démontrer de nouveaux. Il suffit, cependant, de montrer que les axiomes fondamentaux de la géométrie de Lobatchevski sont satisfaits par le modèle de Klein. Les conséquences logiques de la géométrie de Lobatchevski seront alors nécessairement vraies dans le modèle
ALEXANDROV, Alexandre D.
Mathématiques : Leur contenu, leurs méthodes, leur signification
Ainsi avec l’apparition de la sphère formelle à la fin du XIX° siècle la notion de modèle se formalise également. Par ailleurs, la notion de langage se formalise aussi. En effet, quelle que soit la théorie considérée, le langage de celle-ci comporte toujours les éléments suivants :
- des symboles d’objets distingués (appelés aussi symboles d’individus ou de constantes) ;
- des symboles de relations ;
- des symboles d’opérations ;
- des symboles logiques (indépendants de la théorie considérée) : symboles d’objets non-distingués (appelés aussi symbole de génériques ou de variables), symboles de connecteurs et de quantificateurs, parenthèses, virgules, symboles de constantes logiques (tautologique et antilogique).
Le symbole d’égalité peut être, selon le contexte et les auteurs, considéré comme un symbole de relation ou comme un symbole logique. A chaque symbole de relation ![]() (respectivement d’opération
(respectivement d’opération ![]() ) on associe un entier naturel non nul noté
) on associe un entier naturel non nul noté ![]() (respectivement
(respectivement ![]() ) qui est le nombre d’arguments de
) qui est le nombre d’arguments de ![]() (respectivement de
(respectivement de ![]() ). Le symbole
). Le symbole ![]() (respectivement
(respectivement ![]() ) est appelé arité de
) est appelé arité de ![]() (respectivement de
(respectivement de ![]() ).
).
Il est donc parfois possible d’effectuer une traduction d’un langage ![]() dans un langage
dans un langage ![]() sous réserve que
sous réserve que ![]() soit au moins aussi « expressif » que
soit au moins aussi « expressif » que ![]() (c’est-à-dire que
(c’est-à-dire que ![]() puisse coder les symboles d’objets distingués, de relations et d’opérations de
puisse coder les symboles d’objets distingués, de relations et d’opérations de ![]() ).
).
Considérons une théorie formelle ![]() . La théorie
. La théorie ![]() est un ensemble d’énoncés « prouvables » composés :
est un ensemble d’énoncés « prouvables » composés :
- des axiomes formant un système (appelé aussi base) axiomatique
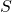 .
.
- Des théorèmes déduits des axiomes de ce système
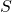 .
.
Pour pouvoir disposer d’un « modèle formel » de ![]() , il faut avoir une théorie
, il faut avoir une théorie ![]() capable de coder tous les symboles d’objet distingué, de relation et d’opération de
capable de coder tous les symboles d’objet distingué, de relation et d’opération de ![]() . Il y a une théorie
. Il y a une théorie ![]() qui s’est naturellement imposée car son langage formel permet de coder par des ensembles les symboles d’objets distingués, de relations et d’individus de toutes les théories mathématiques connues : c’est la théorie des ensembles des mathématiciens allemands Ernst Zermelo (1871 – 1953) et Abraham A.H. Fraenkel (1891 – 1965) développée entre 1908 et 1920.
qui s’est naturellement imposée car son langage formel permet de coder par des ensembles les symboles d’objets distingués, de relations et d’individus de toutes les théories mathématiques connues : c’est la théorie des ensembles des mathématiciens allemands Ernst Zermelo (1871 – 1953) et Abraham A.H. Fraenkel (1891 – 1965) développée entre 1908 et 1920.
La cohérence de cette théorie ne peut pas être démontrée mais un siècle de pratique n’a jamais conduit à prouver et réfuter un même énoncé de la théorie de Zermelo-Fraenkel (appelée théorie ZF). Les mathématiciens estiment donc qu’il est raisonnable de « miser » sur la cohérence de cette théorie. La disponibilité de cette « supra-théorie » permet aux mathématiciens d’avoir un succédané à la notion perdue avec la formalisation : la vérité d’un énoncé. La plupart des mathématiciens considèrent qu’une interprétation ensembliste d’un énoncé est vraie si elle est déductible, au moyen de la logique classique, des axiomes de la théorie de Zermelo-Fraenkel, éventuellement munie d’axiomes additionnels (axiome du choix, hypothèse du continu, axiomes de grands cardinaux, …). Ces axiomes additionnels sont chacun des énoncés indécidables de la théorie de Zermelo-Fraenkel.
À ce stade, il convient maintenant de préciser ce que l’on entend par « interprétation ensembliste » d’un énoncé. Nous allons pour cela introduire deux nouvelles notions :
■ celle de structure d’un langage formel ![]() . Si l’on note :
. Si l’on note :![]() l’ensemble des symboles d’objets distingués de
l’ensemble des symboles d’objets distingués de ![]() ,
,![]() l’ensemble des symboles de relation de
l’ensemble des symboles de relation de ![]() et
et![]() l’ensemble des symboles d’opération de
l’ensemble des symboles d’opération de ![]() .
.
Une structure ![]() est la donnée d’un quadruplet
est la donnée d’un quadruplet ![]() où :
où :
– ![]() est un ensemble appelé domaine de
est un ensemble appelé domaine de ![]() .
.
– ![]() est une application de
est une application de ![]() dans
dans ![]()
– ![]() est une application de
est une application de ![]() dans l’ensemble des relations sur
dans l’ensemble des relations sur ![]()
– ![]() est une application de
est une application de ![]() dans l’ensemble des opérations sur
dans l’ensemble des opérations sur ![]()
Pour tout ![]() de
de ![]() ,
, ![]() est appelée l’interprétation de
est appelée l’interprétation de ![]() dans
dans ![]() et est notée
et est notée ![]()
Pour tout ![]() de
de ![]() ,
, ![]() est appelée l’interprétation de
est appelée l’interprétation de ![]() dans
dans ![]() et est notée
et est notée ![]() . La relation
. La relation ![]() a même arité que
a même arité que ![]() .
.
Pour tout ![]() de
de ![]() ,
, ![]() est appelée l’interprétation de
est appelée l’interprétation de ![]() dans
dans ![]() et est notée
et est notée ![]() . L’interprétation
. L’interprétation ![]() a même arité que
a même arité que ![]() .
.
Les fonctions ![]() ,
, ![]() et
et ![]() ne sont pas nécessairement injectives. Deux symboles distincts (mais de même type) de
ne sont pas nécessairement injectives. Deux symboles distincts (mais de même type) de ![]() peuvent avoir la même interprétation dans
peuvent avoir la même interprétation dans ![]() .
.
■ celle de morphisme d’une structure ![]() de
de ![]() de domaine
de domaine ![]() dans une structure
dans une structure ![]() de
de ![]() de domaine
de domaine ![]()
Si l’on note à nouveau :![]() l’ensemble des symboles d’objets distingués de
l’ensemble des symboles d’objets distingués de ![]()
![]() l’ensemble des symboles de relation de
l’ensemble des symboles de relation de ![]()
![]() l’ensemble des symboles d’opération de
l’ensemble des symboles d’opération de ![]() .
.
On appelle morphisme d’une structure ![]() de
de ![]() de domaine
de domaine ![]() dans une structure
dans une structure ![]() de
de ![]() de domaine
de domaine ![]() toute application
toute application ![]() de
de ![]() dans
dans ![]() telle que :
telle que :
– Pour tout ![]() de
de ![]() , pour tout
, pour tout ![]() de
de ![]() , si on a
, si on a ![]() alors on a
alors on a ![]() . En particulier, si
. En particulier, si ![]() est un symbole de relation binaire
est un symbole de relation binaire ![]() , on aura :
, on aura :
![]()
– Pour tout
En particulier, si
![]()
– pour tout symbole d’objet distingué
Un isomorphisme de ![]() sur
sur ![]() est un morphisme bijectif de
est un morphisme bijectif de ![]() sur
sur ![]() dont la réciproque est un morphisme de
dont la réciproque est un morphisme de ![]() sur
sur ![]() . S’il existe un isomorphisme d’une structure
. S’il existe un isomorphisme d’une structure ![]() sur une structure
sur une structure ![]() , on dit que
, on dit que ![]() et
et ![]() sont isomorphes.
sont isomorphes.
Une structure d’une théorie ![]() est une structure de son langage formel. Elle permet l’interprétation des énoncés de
est une structure de son langage formel. Elle permet l’interprétation des énoncés de ![]() et en particulier des axiomes de
et en particulier des axiomes de ![]() . Si ces axiomes sont de plus des théorèmes de la théorie des ensembles (et si son domaine est non vide) alors la structure est un modèle de
. Si ces axiomes sont de plus des théorèmes de la théorie des ensembles (et si son domaine est non vide) alors la structure est un modèle de ![]() .
.
Il est également important de préciser ce que l’on entend par l’interprétation d’un énoncé ![]() d’un langage formel
d’un langage formel ![]() dans une structure
dans une structure ![]() . L’interprétation
. L’interprétation ![]() de
de ![]() dans
dans ![]() est un énoncé du langage
est un énoncé du langage ![]() de la théorie des ensembles qui est obtenu en remplaçant dans
de la théorie des ensembles qui est obtenu en remplaçant dans ![]() chaque symbole d’objets distingués, de relations et d’opérations par son interprétation respective. Les symboles logiques de
chaque symbole d’objets distingués, de relations et d’opérations par son interprétation respective. Les symboles logiques de ![]() et
et ![]() étant identiques (l’un de ces deux langages peut éventuellement ne pas contenir la relation d’égalité), les symboles logiques de
étant identiques (l’un de ces deux langages peut éventuellement ne pas contenir la relation d’égalité), les symboles logiques de ![]() et
et ![]() sont identiques et occupent les mêmes positions. Cependant les quantifications ne se font plus « à vide » mais dans le domaine
sont identiques et occupent les mêmes positions. Cependant les quantifications ne se font plus « à vide » mais dans le domaine ![]() .
.
Considérons maintenant quelques exemples. Pour chacun d’eux, on verra que ![]() peut contenir ou ne pas contenir le symbole d’égalité. S’il contient le symbole d’égalité alors ce sont les axiomes spécifiques de la théorie qui donne le sens (c’est-à-dire donne les règles d’usage) de ce symbole.
peut contenir ou ne pas contenir le symbole d’égalité. S’il contient le symbole d’égalité alors ce sont les axiomes spécifiques de la théorie qui donne le sens (c’est-à-dire donne les règles d’usage) de ce symbole.
S’il ne contient pas le symbole d’égalité alors ce dernier est un symbole logique dont le sens est donné dans les axiomes du système déductif2, c’est-à-dire par les axiomes logiques.
Exemple 1 : Considérons la théorie des symétries ![]() . Le langage formel
. Le langage formel ![]() de cette théorie est tel que :
de cette théorie est tel que : ![]() ou
ou ![]() , où
, où ![]() est une opération binaire et
est une opération binaire et ![]() est une opération singulaire (i.e d’arité 1).
est une opération singulaire (i.e d’arité 1).
Le langage ![]() permet donc de former par exemple l’expression suivante :
permet donc de former par exemple l’expression suivante : ![]() .
.
La base axiomatique de ![]() est constituée des trois axiomes suivants :
est constituée des trois axiomes suivants :
Axiome 1 : Pour tous ![]() et
et ![]() ,
, ![]() .
.
Axiome 2 : Pour tout ![]() ,
, ![]() .
.
Axiome 3 : Pour tout ![]() ,
, ![]() .
.
Une structure ![]() de
de ![]() dans laquelle les 4 axiomes précédents sont prouvables dans ZF est un modèle de
dans laquelle les 4 axiomes précédents sont prouvables dans ZF est un modèle de ![]() . Le quadruplet
. Le quadruplet ![]() est alors appelé groupe. Il est souvent noté plus simplement sous la forme du couple
est alors appelé groupe. Il est souvent noté plus simplement sous la forme du couple ![]() .
.
Un groupe est donc un ensemble ![]() muni d’une loi de composition interne
muni d’une loi de composition interne ![]() telle que :
telle que :
i) Pour tout élément ![]() et
et ![]() de
de ![]() ,
, ![]() .
.
ii) Il existe un élément ![]() de
de ![]() telle que pour tout élément
telle que pour tout élément ![]() de
de ![]() ,
, ![]() .
.
iii) Pour tout élément ![]() de
de ![]() , il existe un élément
, il existe un élément ![]() de
de ![]() telle que
telle que ![]() . L’élément
. L’élément ![]() est noté
est noté ![]() .
.
Dans un groupe, l’expression ![]() est donc simplifiable. On a :
est donc simplifiable. On a : ![]() .
.
Il existe de nombreux modèles pour ![]() :
: ![]()
Un morphisme du groupe ![]() dans le groupe
dans le groupe ![]() est une application
est une application ![]() de
de ![]() dans
dans ![]() telle que :
telle que :
1) ![]()
2) Pour tous ![]() de
de ![]() ,
, ![]() .
.
3) Pour chaque ![]() de
de ![]() ,
, ![]() .
.
Par exemple, la fonction exponentielle est un morphisme du groupe ![]() dans le groupe
dans le groupe ![]() .
.
Il est facile de montrer qu’ici la condition 2) implique nécessairement les conditions 1) et 3).
C’est pourquoi cette définition équivaut à la définition classique d’un morphisme de groupe qui ne fait intervenir que la condition 2)
Remarque : Un isomorphisme d’une structure ![]() sur elle-même est appelé automorphisme de
sur elle-même est appelé automorphisme de ![]() .
.
Une telle application ne fait que modifier la « place » des éléments du domaine de la structure sans modifier « la forme » de la structure. La théorie formelle des symétries ![]() trouve son origine dans la sphère idéale ou formelle. Dans ces deux sphères, une symétrie est une transformation de l’espace (i.e une transformation ponctuelle inversible) agissant sur un objet géométrique ou physique en préservant des propriétés géométriques (les dimensions, les angles, le volume …) ou des propriétés physiques (masse, charge électrique, …). La notion d’automorphisme de structure est donc un « pendant formel ensembliste » de la notion de symétrie. On vérifie d’ailleurs facilement que l’ensemble des automorphismes d’une structure
trouve son origine dans la sphère idéale ou formelle. Dans ces deux sphères, une symétrie est une transformation de l’espace (i.e une transformation ponctuelle inversible) agissant sur un objet géométrique ou physique en préservant des propriétés géométriques (les dimensions, les angles, le volume …) ou des propriétés physiques (masse, charge électrique, …). La notion d’automorphisme de structure est donc un « pendant formel ensembliste » de la notion de symétrie. On vérifie d’ailleurs facilement que l’ensemble des automorphismes d’une structure ![]() de domaine
de domaine ![]() muni de la loi de composition des applications de
muni de la loi de composition des applications de ![]() dans lui-même est un groupe !
dans lui-même est un groupe !
Exemple 2 : Considérons la théorie de l’ordre total ![]() .
.
Le langage formel ![]() de cette théorie est tel que :
de cette théorie est tel que : ![]() ,
, ![]() ou
ou ![]() ,
, ![]() .
.![]() est une relation binaire. Cette théorie comporte 4 axiomes :
est une relation binaire. Cette théorie comporte 4 axiomes :
Axiome 1 : Pour tous ![]() , si
, si ![]() et
et ![]() alors
alors ![]() .
.
Axiome 2 : Pour tous ![]() , si
, si ![]() et
et ![]() alors
alors ![]() .
.
Axiome 3 : Pour tout ![]() ,
, ![]() .
.
Axiome 4 : Pour tous ![]() ,
, ![]() ou
ou ![]() .
.
Une structure ![]() de
de ![]() dans laquelle les 4 axiomes précédents sont prouvables dans ZF est un modèle ensembliste de
dans laquelle les 4 axiomes précédents sont prouvables dans ZF est un modèle ensembliste de ![]() . Le quadruplet
. Le quadruplet ![]() est appelé ensemble totalement ordonné. Il est souvent noté plus simplement sous la forme du couple
est appelé ensemble totalement ordonné. Il est souvent noté plus simplement sous la forme du couple ![]() .
.
Un ensemble totalement ordonné est donc un ensemble ![]() muni d’une relation binaire sur
muni d’une relation binaire sur ![]() notée
notée ![]() telle que :
telle que :
i) Pour tous ![]() de
de ![]() , si
, si ![]() et
et ![]() alors
alors ![]() .
.
ii) Pour tous ![]() de
de ![]() , si
, si ![]() et
et ![]() alors
alors ![]() .
.
iii) Pour tout ![]() de
de ![]() ,
, ![]() .
.
iv) Pour tous ![]() de
de ![]() ,
, ![]() ou
ou ![]() .
.
Il existe de nombreux modèles pour ![]() : Par exemple il y a
: Par exemple il y a ![]() et
et ![]() avec
avec ![]() .
.
Un morphisme de l’ensemble ordonné ![]() dans l’ensemble ordonné
dans l’ensemble ordonné ![]() est une application
est une application ![]() de
de ![]() dans
dans ![]() telle que : pour tous
telle que : pour tous ![]() de
de ![]() ,
, ![]() .
.
Par exemple la fonction exponentielle est un morphisme de l’ensemble totalement ordonné ![]() dans l’ensemble totalement ordonné
dans l’ensemble totalement ordonné ![]()
Remarque : Il arrive que l’on souhaite formaliser une théorie qui, dans les sphères sensible et idéale, comporte plusieurs types d’objets, comme par exemple :
– La théorie de la géométrie de l’espace euclidien qui comporte trois types d’objets : les points, les droites et les plans.
– La théorie des espaces vectoriels qui comporte deux types d’objet : les scalaires et les vecteurs
Il faut alors considérer des symboles de relation singulaire (d’arité 1) distincts. Chacun d’eux permettra ainsi de coder le fait pour un objet d’être « d’un certain type ».
Considérons par exemple la théorie ![]() des espaces vectoriels. Cette théorie comporte deux types d’objets : les scalaires et les vecteurs. On a :
des espaces vectoriels. Cette théorie comporte deux types d’objets : les scalaires et les vecteurs. On a : ![]() ,
, ![]() ou
ou ![]() ,
, ![]() .
.![]() pourra s’interpréter par « être un vecteur » et
pourra s’interpréter par « être un vecteur » et ![]() par « être un scalaire ». Les énoncés
par « être un scalaire ». Les énoncés ![]() ,
, ![]() et
et ![]() seront des axiomes de
seront des axiomes de ![]() .
.
Voici quatre autres axiomes de cette théorie :
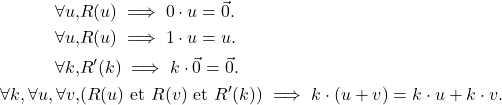
Une structure pour ![]() est appelé structure d’espace vectoriel. Le domaine
est appelé structure d’espace vectoriel. Le domaine ![]() d’une telle structure sera l’ensemble des vecteurs et des scalaires. Si l’on note
d’une telle structure sera l’ensemble des vecteurs et des scalaires. Si l’on note ![]() et
et ![]() les interprétations respectives de
les interprétations respectives de ![]() et
et ![]() et en notant (abusivement dans un but de simplification) de manière identique les symboles d’éléments distingués et d’opérations de
et en notant (abusivement dans un but de simplification) de manière identique les symboles d’éléments distingués et d’opérations de ![]() et leurs interprétations, le quadruplet
et leurs interprétations, le quadruplet ![]() est appelé espace vectoriel. Cet espace vectoriel vérifie en particulier les quatre axiomes suivants :
est appelé espace vectoriel. Cet espace vectoriel vérifie en particulier les quatre axiomes suivants :
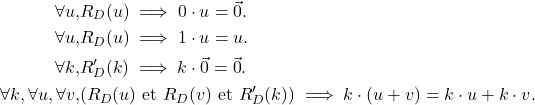
Considérons les ensembles
On a
Nos quatre axiomes pourront alors se noter de manière plus usuelle :
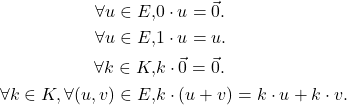
Si on choisit ![]() , on peut définir deux relations singulaires
, on peut définir deux relations singulaires ![]() et
et ![]() sur
sur ![]() par
par
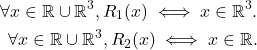
Si de plus on définit deux opérations ![]() et
et ![]() sur
sur ![]() vérifiant :
vérifiant :
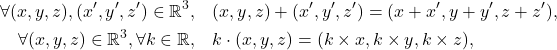
où ![]() et
et ![]() sont l’addition et la multiplication des réels,
sont l’addition et la multiplication des réels,
alors ![]() est un modèle ensembliste de
est un modèle ensembliste de ![]() .
.![]() et
et ![]() ne sont pas des lois de composition interne sur
ne sont pas des lois de composition interne sur ![]() car elles ne sont pas définies sur
car elles ne sont pas définies sur ![]() tout entier (
tout entier (![]() ne peut opérer entre un scalaire et un vecteur,
ne peut opérer entre un scalaire et un vecteur, ![]() ne peut opérer entre deux vecteurs ou entre deux scalaires). On peut cependant les voir comme des lois de composition interne en affectant des valeurs arbitraires aux résultats des opérations « illicites ».
ne peut opérer entre deux vecteurs ou entre deux scalaires). On peut cependant les voir comme des lois de composition interne en affectant des valeurs arbitraires aux résultats des opérations « illicites ».
Une théorie ![]() qui a un modèle est considérée comme cohérente. En effet si
qui a un modèle est considérée comme cohérente. En effet si ![]() était incohérente alors la théorie des ensembles le serait également. On dit que
était incohérente alors la théorie des ensembles le serait également. On dit que ![]() est cohérente relativement à la théorie des ensembles.
est cohérente relativement à la théorie des ensembles. ![]() et
et ![]() sont donc cohérentes (relativement à la théorie des ensembles).
sont donc cohérentes (relativement à la théorie des ensembles).
Deux modèles de ![]() isomorphes sont identiques du point de vue logique. En effet, deux énoncés
isomorphes sont identiques du point de vue logique. En effet, deux énoncés ![]() et
et ![]() de
de ![]() interprétant un même énoncé
interprétant un même énoncé ![]() d’un langage
d’un langage ![]() dans deux structure
dans deux structure ![]() et
et ![]() isomorphes, seront soient tous les deux prouvables, réfutables, indécidables ou contradictoires.
isomorphes, seront soient tous les deux prouvables, réfutables, indécidables ou contradictoires.
Si tous les modèles de ![]() sont isomorphes, on dit que
sont isomorphes, on dit que ![]() est catégorique.
est catégorique.
Exemple 1 : Dans la théorie ![]() considérons l’énoncé
considérons l’énoncé ![]() suivant :
suivant :
![]()
L’interprétation de l’énoncé
Les modèles
Exemple 2 : Dans la théorie ![]() considérons l’énoncé
considérons l’énoncé ![]() suivant :
suivant :
![]()
L’interprétation de l’énoncé
son interprétation dans tous les modèles de
Les modèles
Ainsi la notion de modèle permet de reconnaître certains énoncés indécidables d’une théorie formelle (reconnaissance qui reste relative à la cohérence de la théorie des ensembles).
Le mathématicien allemand Leopold Löwenheim (1878 – 1957) et le mathématicien norvégien Thoraf Skolem (1887 – 1963) ont montré entre 1915 et 1920 qu’une théorie qui admet un modèle dont le domaine est infini n’est pas catégorique.
![]() et
et ![]() admettant des modèles infinis, on retrouve par ce dernier théorème qu’elles ne sont pas catégoriques. Comme la plupart des théories mathématiques admettent un modèle infini, les théories catégoriques sont peu nombreuses. C’est pourquoi les mathématiciens s’intéressent à une forme plus faible de catégoricité : la catégoricité relativement à un cardinal donné
admettant des modèles infinis, on retrouve par ce dernier théorème qu’elles ne sont pas catégoriques. Comme la plupart des théories mathématiques admettent un modèle infini, les théories catégoriques sont peu nombreuses. C’est pourquoi les mathématiciens s’intéressent à une forme plus faible de catégoricité : la catégoricité relativement à un cardinal donné ![]() . Un cardinal fini ou infini
. Un cardinal fini ou infini ![]() étant donné, cela consiste à étudier si tous les modèles de cardinal
étant donné, cela consiste à étudier si tous les modèles de cardinal ![]() d’une théorie
d’une théorie ![]() sont isomorphes. Dans l’affirmative, on dira que
sont isomorphes. Dans l’affirmative, on dira que ![]() est
est ![]() -catégorique. Les modèles dénombrables
-catégorique. Les modèles dénombrables ![]() et
et ![]() de
de ![]() n’étant pas isomorphes,
n’étant pas isomorphes, ![]() n’est pas «
n’est pas « ![]() -catégorique ».
-catégorique ». ![]() n’est pas 4-catégorique (
n’est pas 4-catégorique ( ![]() et
et ![]() ne sont pas isomorphes) mais est
ne sont pas isomorphes) mais est ![]() -catégorique si
-catégorique si ![]() est un entier premier (tous les groupes d’ordre
est un entier premier (tous les groupes d’ordre ![]() premier sont isomorphes à
premier sont isomorphes à ![]() ).
).
Considérons la théorie ![]() des entiers naturels.
des entiers naturels.
Le langage formel ![]() de cette théorie est tel que :
de cette théorie est tel que : ![]() ,
, ![]() ou
ou ![]() ,
, ![]() .
.![]() est une opération singulaire interprétée par « successeur de ». Cette théorie comporte les quatre axiomes suivants :
est une opération singulaire interprétée par « successeur de ». Cette théorie comporte les quatre axiomes suivants :
Axiome 1 : Il n’existe pas ![]() tel que
tel que ![]() .
.
Axiome 2 : Pour tout ![]() ,
, ![]() ou il existe
ou il existe ![]() tel que
tel que ![]() .
.
Axiome 3 : Pour tous ![]() et
et ![]() , si
, si ![]() alors
alors ![]() .
.
Axiome 4 : pour chaque propriété ![]() portant sur
portant sur ![]() , si on a
, si on a ![]() et si pour chaque
et si pour chaque ![]() , quand on a
, quand on a ![]() on a
on a ![]() , alors on a : Pour chaque
, alors on a : Pour chaque ![]() ,
, ![]() .
.
Remarques : L’axiome 4 n’est pas véritablement un axiome mais une collection infinie dénombrable d’axiomes : l’axiome 4 « produit » autant d’axiomes qu’il y a d’énoncés possibles portant sur un entier naturel ![]() . L’axiome 4 est en fait ce que l’on appelle un « schéma d’axiomes ». L’axiome 2 peut être éliminé : il peut en effet être déduit des autres axiomes.
. L’axiome 4 est en fait ce que l’on appelle un « schéma d’axiomes ». L’axiome 2 peut être éliminé : il peut en effet être déduit des autres axiomes.
L’ensemble ![]() est un modèle de
est un modèle de ![]() .
. ![]() est donc cohérente (relativement à la théorie des ensembles). Ce modèle étant infini,
est donc cohérente (relativement à la théorie des ensembles). Ce modèle étant infini, ![]() n’est pas catégorique.
n’est pas catégorique.
Les modèles de ![]() isomorphes à
isomorphes à ![]() sont appelés modèles standards de
sont appelés modèles standards de ![]() .
.
On peut montrer que tout modèle non-standard de ![]() « contient »
« contient » ![]() .
.
Un modèle non-standard de![]() peut être dénombrable ou non.
peut être dénombrable ou non.
Mais qu’appelle-ton ![]() ? Puisque
? Puisque ![]() est un modèle de
est un modèle de ![]() cela signifie que
cela signifie que ![]() est un ensemble tel
est un ensemble tel
– qu’il existe un élément de ![]() qui interprète
qui interprète ![]() .
.
– qu’il existe une application ![]() de
de ![]() dans
dans ![]() qui interprète
qui interprète ![]() .
.
– que l’interprétation des axiomes de ![]() sont des théorèmes de la théorie de Zermelo-Fraenkel.
sont des théorèmes de la théorie de Zermelo-Fraenkel.
Il existe plusieurs choix possibles pour les interprétations de ![]() et
et ![]() . Le mathématicien américano-hongrois John Von Neumann (1903 – 1957) proposa d’interpréter
. Le mathématicien américano-hongrois John Von Neumann (1903 – 1957) proposa d’interpréter ![]() par l’ensemble vide
par l’ensemble vide ![]() et
et ![]() par l’application
par l’application ![]() qui à tout ensemble
qui à tout ensemble ![]() associe l’ensemble
associe l’ensemble ![]() .
.
Ainsi ![]() s’interprète par
s’interprète par ![]() ,
, ![]() par
par ![]() … On pose alors
… On pose alors ![]()
Cela ne signifie pas que l’entier ![]() est l’ensemble
est l’ensemble ![]() .
.![]() n’est qu’une interprétation ensembliste de l’entier
n’est qu’une interprétation ensembliste de l’entier ![]() .
.
Nous avons vu qu’une théorie formelle qui admet un modèle est cohérente (relativement à la théorie des ensembles). Un théorème de Kurt Gödel, publié en 1929 dans sa thèse de doctorat, appelé « Théorème de complétude », affirme que toute théorie formelle cohérente admet un modèle.
Nous en déduisons que si la théorie ZF est cohérente, elle doit donc admettre elle-même un modèle.
La théorie des ensembles peut donc alors être interprétée dans une structure ![]() où
où ![]() est un ensemble et
est un ensemble et ![]() est une relation binaire sur
est une relation binaire sur ![]() interprétant la relation d’appartenance
interprétant la relation d’appartenance ![]() .
.
Or Kurt Gödel a montré en 1931 un autre théorème, appelé « Théorème d’incomplétude », qui a pour conséquence que la théorie des ensembles ne peut prouver sa propre cohérence. Il n’est donc pas possible de construire ![]() à partir des axiomes de ZF.
à partir des axiomes de ZF.
- La terminologie « classe ouverte» est due au mathématicien suisse Ferdinand Gonseth. ↩︎
- Il s’agit des axiomes de réflexivité, de symétrie, de transitivité et du schéma d’axiomes de substitution. ↩︎
Remerciements
L’auteur de cet exposé tient à remercier :
1) Marc Sage pour lui avoir fait découvrir le livre de Ferdinand Gonseth « Les mathématiques et la réalité », pour avoir répondu par mail à ses nombreuses questions sur la logique mathématique et pour avoir contribué par ses relectures à l’amélioration de cet exposé.
2) Samuel Petite (Directeur de l’IREM de Picardie et Professeur des Universités à l’UPJV) pour l’intérêt porté à cet exposé et pour avoir permis sa relecture par un rapporteur.
3) Guillaume Malod (Maître de Conférence à l’IMJ-PRG (équipe Logique) et membre de l’IREM de Paris) pour avoir accepté de relire cet exposé.
Bibliographie
Le présent document comporte de nombreux extraits des deux livres suivants :
[1] ALEXANDROV, Alexandre D. Mathématiques : Leur contenu, leurs méthodes, leur signification
Autres auteurs : KOLMOGOROV, Andreï N. ; LAVRENTIEV, Mikhaïl
Traducteur : CABANNES, André
Editions du Bec de l’Aigle, 2020
Volume 1 : 520 p. ISBN 9782957239122
Volume 2 : 678 P. ISBN 9782957239115
Volume 3 : 583 p. ISBN 9782957239139
[2] GONSETH, Ferdinand. Les mathématiques et la réalité : Essai sur la méthode axiomatique
Albert Blanchard, 2000. 386 p. ISBN 9782853671125
On trouvera également dans cet exposé des extraits des ouvrages suivants :
[3] EINSTEIN, Albert. La relativité
Traducteur : SOLOVINE, Maurice
Payot, 1990. 240 p. ISBN 9782228882545
[4] HUME, David. Enquête sur l’entendement humain
Traducteur : MALHERBE, Michel
Vrin, 2008. 420 p. ISBN 9782711619900
Je n’ai pas utilisé d’ouvrages édités sur la théorie des modèles. J’ai (très ponctuellement) utilisé les polycopiés universitaires suivants que l’on trouvera au format pdf sur la page web de leur auteur.
[5] ROZIERE, Paul. Introduction à la logique mathématique
Université Paris VII, 2004. 75 p.
[6] CHATZIDAKIS, Zoé. Introduction à la logique
Ecole Normale Supérieure, 2015. 120 p.